Frequency analysis
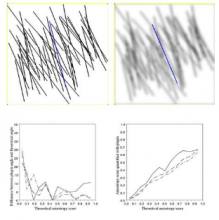
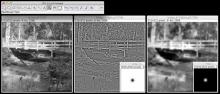
https://en.wikipedia.org/wiki/Fourier_analysis https://en.wikipedia.org/wiki/Wavelet|Frequency domain analysis (or spectral density estimation), is the process of decomposing a complex signal into simpler parts. Many physical processes are best described as a sum of many individual frequency components. Any process that quantifies the various amounts (e.g. amplitudes, powers, intensities, or phases), versus frequency can be called spectrum analysis. The Fourier transform of a function produces its frequency spectrum by decomposing the function into its sine and cosine components. Whereas the standard Fourier transform is only localized in frequency, wavelets are localized in both time and frequency. Wavelets are handcrafted to correlate with particular frequencies in a signal; a set of wavelets is usually used for a complete analysis.